La teoría de grafos (también llamada teoría de las gráficas)
es un campo de estudio de las matemáticas y las ciencias de la computación, que
estudia las propiedades de los grafos (también llamadas gráficas, que no se
debe confundir con las gráficas que tienen una acepción muy amplia) estructuras
que constan de dos partes, el conjunto de vértices, nodos o puntos; y el
conjunto de aristas, líneas o lados (edges en inglés) que pueden ser orientados
o no. Por lo tanto también esta conocido como análisis de redes.
La teoría de grafos es una rama de las matemáticas discretas
y de las matemáticas aplicadas, y es un tratado que usa diferentes conceptos de
diversas áreas como combinatoria, álgebra, probabilidad, geometría de
polígonos, aritmética y topología.
Actualmente ha tenido mayor preponderancia en el campo de la
informática, las ciencias de la computación y telecomunicaciones.
HISTORIA.
El origen de la teoría de grafos se remonta al siglo XVIII
con el problema de los puentes de Königsberg, el cual consistía en encontrar un
camino que recorriera los siete puentes del río Pregel (54°42'12?N 20°30'56?E)
en la ciudad de Königsberg, actualmente Kaliningrado, de modo que se
recorrieran todos los puentes pasando una sola vez por cada uno de ellos. El
trabajo de Leonhard Euler sobre el problema titulado Solutio problematis ad
geometriam situs pertinentis2 (La solución de un problema relativo a la
geometría de la posición) en 1736, es considerado el primer resultado de la
teoría de grafos. También se considera uno de los primeros resultados
topológicos en geometría (que no depende de ninguna medida). Este ejemplo
ilustra la profunda relación entre la teoría de grafos y la topología.
Luego, en 1847, Gustav Kirchhoff utilizó la teoría de grafos
para el análisis de redes eléctricas publicando sus leyes de los circuitos para
calcular el voltaje y la corriente en los circuitos eléctricos, conocidas como
leyes de Kirchhoff, considerado la primera aplicación de la teoría de grafos a
un problema de ingeniería.
En 1852 Francis Guthrie planteó el problema de los cuatro
colores el cual afirma que es posible, utilizando solamente cuatro colores,
colorear cualquier mapa de países de tal forma que dos países vecinos nunca
tengan el mismo color. Este problema, que no fue resuelto hasta un siglo
después por Kenneth Appel y Wolfgang Haken en 1976, puede ser considerado como
el nacimiento de la teoría de grafos. Al tratar de resolverlo, los matemáticos
definieron términos y conceptos teóricos fundamentales de los grafos.
En 1857, Arthur Cayley estudió y resolvió el
problema de enumeración de los isómeros, compuestos químicos con idéntica
composición (fórmula) pero diferente estructura molecular. Para ello representó
cada compuesto, en este caso hidrocarburos saturados CnH2n+2, mediante
un grafo árbol donde los vértices representan átomos y las
aristas la existencia de enlaces químicos.
El término «grafo», proviene de la expresión H«graphic
notation» usada por primera vez por Edward Frankland3 y posteriormente adoptada
por Alexander Crum Brown en 1884, y hacía referencia a la representación
gráfica de los enlaces entre los átomos de una molécula.
El primer libro sobre teoría de grafos fue escrito por Dénes
Konig y publicado en 1936
APLICACIONES.
Gracias a la teoría de grafos se pueden resolver diversos
problemas como por ejemplo la síntesis de circuitos secuenciales, contadores o
sistemas de apertura. Se utiliza para diferentes áreas por ejemplo, Dibujo
computacional, en toda las áreas de Ingeniería.
Los grafos se utilizan también para modelar trayectos como
el de una línea de autobús a través de las calles de una ciudad, en el que
podemos obtener caminos óptimos para el trayecto aplicando diversos algoritmos
como puede ser el algoritmo de Floyd.
Para la administración de proyectos, utilizamos técnicas
como técnica de revisión y evaluación de programas (PERT) en las que se modelan
los mismos utilizando grafos y optimizando los tiempos para concretar los
mismos.
La teoría de grafos también ha servido de
inspiración para las ciencias sociales, en especial para desarrollar un
concepto no metafórico de red social que sustituye los nodos por los actores
sociales y verifica la posición, centralidad e importancia de cada actor dentro
de la red. Esta medida permite cuantificar y abstraer relaciones complejas, de
manera que la estructura social puede representarse gráficamente. Por ejemplo,
una red social puede representar la estructura de poder dentro de una sociedad al identificar los vínculos
(aristas), su dirección e intensidad y da idea de la manera en que el poder se
transmite y a quiénes.
Se emplea en problemas de control de producción, para
proyectar redes de ordenadores, para diseñar módulos electrónicos modernos y
proyectar sistemas físicos con parámetros localizados (mecánicos, acústicos y
eléctricos).
Se usa para la solución de problemas de genética y problemas
de automatización de la proyección (SAPR). Apoyo matemático de los sistemas
modernos para el procesamiento de la información. Acude en las investigaciones
nucleares (técnica de diagramas de Feynman).5
Los grafos son importantes en el estudio de la biología y
hábitat. El vértice representa un hábitat y las aristas (o "edges" en
inglés) representa los senderos de los animales o las migraciones. Con esta
información, los científicos pueden entender cómo esto puede cambiar o afectar
a las especies en su hábitat.
TIPOS DE GRAFOS .
Grafo simple. o
simplemente grafo es aquel que acepta una sola arista uniendo dos vértices
cualesquiera. Esto es equivalente a decir que una arista cualquiera es la única
que une dos vértices específicos. Es la definición estándar de un grafo.
Multigrafo. o
pseudografo son grafos que aceptan más de una arista entre dos vértices.
Estas aristas se llaman múltiples o lazos (loops en inglés). Los grafos simples
son una subclase de esta categoría de grafos. También se les llama grafos
no-dirigido.
Grafo dirigido.
Son grafos en los cuales se ha añadido una orientación a las aristas,
representada gráficamente por una flecha.
Grafo etiquetado. Grafos en los cuales se ha añadido un peso a
las aristas (número entero generalmente) o un etiquetado a los vértices.
Grafo aleatorio.
Grafo cuyas aristas están asociadas a una probabilidad.
Hipergrafo. Grafos en los cuales las aristas tienen más de
dos extremos, es decir, las aristas son incidentes a 3 o más vértices
Grafo infinito.
Grafos con conjunto de vértices y aristas de cardinal infinito.
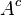(que se lee A complemento), al conjunto
