Relación de conjuntos: pertenencia, inclusión, igualdad y diferencia.

Pertenencia: Cuando un elemento integra un conjunto, se dice que el elemento pertenece al conjunto y se denota por ϵ y en caso contrario se denota por ϵ.

Ejemplo:

Inclusión:  Un conjunto está incluido en otro conjunto cuando todos sus elementos también pertenecen al otro conjunto. La inclusión se denota por C y caso contrario por C.

Ejemplo:

B = {1,2,3,4,5,6,7,8}   y    A = {2,3,6,8}
Todos los elementos de A son también de B. Decimos entonces que “A está incluido en B” o que “A es subconjunto de B”. A  C  B.

Definición: Sean A y B dos subconjuntos. Decimos que A es subconjunto de B, A  C  B, si y sólo si todo elemento de A es también elemento de B, simbólicamente A  C  B  <=> Para todo x (x ϵ A=> x ϵ B).

 

Igualdad: Dos conjuntos A y B son iguales si tienen exactamente los mismos elementos.

En símbolos A = B <=> (x ϵ A => x ϵ B) ^ (x ϵ B => x ϵ A)

Es decir: Todo elemento de A pertenece a B y todo elemento de B pertenece a A.

Ejemplo:

Diferencia de conjuntos: 

En términos prácticos, el complemento de un conjunto es todo lo que no está en el conjunto.

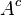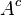Sea A un conjunto dentro de un conjunto universo U. Se define el complemento de A, denotado por (que se lee A complemento), al conjunto

Ejemplo:

Si realizas la operación M menos N, debes seleccionar los elementos de M que no están en N.  Representamos la diferencia M menos N así: M \ N.  Observa que en este caso M \ N={a,c}.